Desde el inicio de la pandemia ocasionada por el virus SARS-CoV-2 contamos y medimos sin descanso. Cada día recibimos cantidades ingentes de información en forma de gráficos, tablas e infografías, y hemos incorporado a nuestro vocabulario expresiones como ritmo de contagio, aplanar la curva o crecimiento exponencial. Los investigadores Manuel de León y Antonio Gómez Corral presentan las matemáticas que hay detrás de estos términos en el último libro de la colección ‘¿Qué sabemos de?’ (CSIC-Catarata). Las matemáticas de la pandemia recoge las herramientas que se utilizan para comprender el proceso de transmisión de enfermedades como la viruela, la malaria o la COVID-19 y expone cómo esta disciplina ayuda a diseñar medidas para combatirlas.
El texto explica uno de los instrumentos básicos con los que trabaja la comunidad científica para conocer el impacto de una epidemia: el número de reproducción básico, Ro. Se trata de un parámetro teórico que hace referencia al número medio de contagios generados por una persona contagiada. El valor de Ro depende de múltiples aspectos, como las condiciones ambientales o lo susceptible que sea la población al patógeno. Por eso este parámetro se complementa con el número de reproducción efectivo Re, que tiene en cuenta factores como si algunas personas están vacunadas contra la enfermedad o si tienen inmunidad debido a que previamente estuvieron expuestas al patógeno. “El valor Re es menor que el número de reproducción básico Ro, es dinámico, es decir, cambia con el tiempo y, por lo tanto, es un estimador del potencial de propagación más realista que Ro”, declaran los autores. Por ejemplo, “las estrategias de intervención como el lavado de manos, el distanciamiento social, el aislamiento y la cuarentena aplicadas durante la pandemia de SARS en 2003 permitieron reducir el valor 2,5 inicial del factor de reproducción básico Ro a un valor Re por debajo de 1 tras dos meses de estricta aplicación”, aclaran.
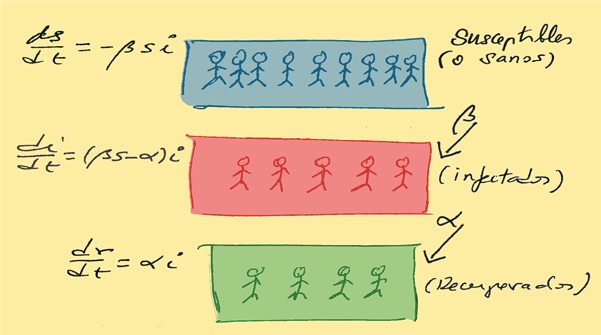
El modelo SIR y sus fortalezas
Los modelos constituyen otra de las herramientas matemáticas más utilizadas para estudiar epidemias. El libro ocupa buena parte de sus páginas en contar el modelo SIR. Su nombre alude a los tres grupos en los que se clasifican individuos de una población según su estado ante una enfermedad: susceptible (S), infectado (I) y resistente o recuperado (R).
Formulado hace casi un siglo, el modelo está basado en ecuaciones diferenciales y dio respuestas a preguntas como ¿por qué finaliza una epidemia? o ¿por qué aparecen brotes aleatorios? En la actualidad sigue siendo una referencia en epidemiología matemática, aunque para la pandemia actual solo sea un punto de partida. Según Manuel de León y Antonio Gómez Corral, en el caso del SARS-CoV-2, uno de los desafíos es determinar el tiempo en el que una persona infectada es asintomática pero puede infectar a otras susceptibles. “Para acomodar mejor esta circunstancia en el modelo, la variante SEIR incluye un estado intermedio, denotado por E (abreviatura de expuesto), que trata de simular ese periodo de latencia o incubación”. Este modelo introduce mucha flexibilidad al incorporar dos nuevos parámetros: el tiempo medio de latencia y la probabilidad de que un individuo asintomático sea infeccioso y es, hasta el momento, el más utilizado para hacer predicciones cuantitativas sobre la COVID-19.
El libro también da cuenta de otras variantes del modelo SIR que contemplan a los individuos tratados o en cuarentena. Sin embargo, incluir más elementos no siempre es garantía de éxito, ya que “los modelos complejos traen consigo una mayor incertidumbre en sus parámetros, y por ello pueden limitar su utilidad predictiva, así que no siempre son preferidos frente a otros más sencillos”, afirman los matemáticos. “Con seguridad, el modelo SIR estará muy alejado de una realidad que, por ahora y hasta que la pandemia provocada por SARS-CoV-2 se estabilice, no conoceremos con detalle”, añaden.
El trabajo multidisciplinar continúa en este ámbito y en España ya existen iniciativas para desarrollar modelos matemáticos más precisos que permitan evaluar el impacto de las medidas adoptadas para controlar la pandemia actual.
Series temporales
Junto con herramientas determinísticas construidas desde ecuaciones diferenciales como el modelo SIR y otras basadas en la teoría de probabilidad, existen técnicas muy útiles como las series temporales que se centran en el uso dinámico de los datos acumulados.
“Una serie temporal no es más que una colección de datos recogidos en instantes de tiempo equidistantes (por ejemplo, los litros de lluvia recogidos cada día en un determinado lugar o el número de fallecidos por COVID-19 confirmados cada día en una comunidad autónoma)”, comentan los investigadores. Con una serie temporal se intenta tener una buena comprensión de lo que ha ocurrido en el pasado y aprovechar ese conocimiento para predecir el futuro.
Calidad y rapidez de los datos: la asignatura pendiente
Sobre las lecciones aprendidas durante la pandemia actual, los autores ponen el foco en la rapidez de acceso a los datos y en su calidad para hacer posible un análisis adecuado. “Sean cuales sean las características y peculiaridades que se incorporen al modelo matemático que describa la propagación del SARS-CoV-2, sus virtudes y limitaciones estarán siempre marcadas por los datos que lo soporten, es decir, que permitan su construcción y validación”. Por eso, Manuel de León y Antonio Gómez Corral abogan por “un procedimiento de recolección de datos único, estandarizado —no solo en el ámbito español, sino incluso en el europeo o en el mundial, bajo directrices de la OMS— y, lo más importante, ágil en su ejecución y que permita el acceso rápido de los investigadores interesados bajo las correspondientes premisas éticas y de uso responsable”, concluyen.
Las matemáticas de la pandemia es el número 118 de la colección de divulgación ‘¿Qué sabemos de?’ (CSIC-Catarata). El libro puede adquirirse tanto en librerías como en las páginas web de Editorial CSIC y Los Libros de la Catarata.
Sobre los autores
Manuel de León es matemático, profesor de investigación del CSIC y fundador del Instituto de Ciencias Matemáticas. Ha sido miembro del Comité Ejecutivo de la Unión Matemática Internacional (IMU) y del Consejo Internacional de la Ciencia (ICSU).
Antonio Gómez Corral es matemático y profesor de la UCM. Sus intereses científicos, tanto de investigación como de divulgación, se centran en las aplicaciones de los procesos estocásticos a problemas biológicos, en especial a la propagación de enfermedades transmisibles.
CSIC Comunicación / CSIC Cultura Científica